※アイキャッチ画像は本家から拝借しています。
前回の Operational principles に続いて、今回は Low-rents の解読と勉強。図は本家から拝借しています。
Low-rents
Low-rentsは、Mutable Instruments Streams の Easter egg にある Lorenz アトラクター*1・モジュレーション・ジェネレーターを移植したもので、これに Rössler アトラクター*1が追加されている。
2つの独立したファンクション・ジェネレーター(ここでは「ジェネレーター 1」 と「ジェネレーター 2」 と呼ぶ)が用意されており、各ジェネレーターは同じ位相累算器(アキュムレーター accumulator)*2を使用して、Lorenz 関数と Rössler 関数の両方を同時に計算するが、各ジェネレーターのレートおよびスピードは独立して設定可能。Lorenz 関数も Rössler 関数も 3 つの値(x、y、z)を出力し、これらの様々な組み合わせを 4 つの出力チャンネルにマッピングすることができる。カオティックなストレンジアトラクター*3は、低速変調機能として最適。
o_C モジュールの出力電圧範囲は、ピッチCVを処理するように設計されているため、非対称(約-3V~+6V)であることに注意が必要。Low-rents アプリの出力は 0V を中心としたものではない。
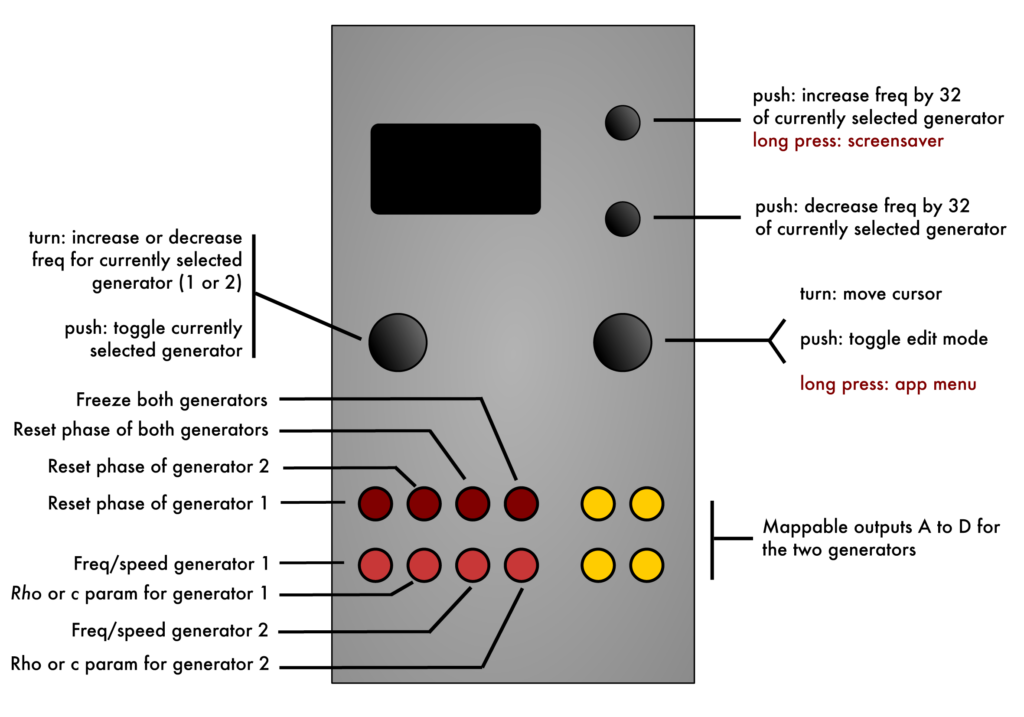
| I/O | 機能 |
|---|---|
| TR1 | ジェネレーター 1 の位相リセット |
| TR2 | ジェネレーター 2 の位相リセット |
| TR3 | 両方のジェネレーターの位相リセット |
| TR4 | フリーズ(TR4 のパルスが High の間、両方のジェネレーターが停止し、停止時点での電圧値を保持) |
| CV1 | ジェネレーター 1 の周波数/速度 |
| CV2 | ジェネレーター 1 の Rho または c パラメータ |
| CV3 | ジェネレーター 2 の周波数/速度 |
| CV4 | ジェネレーター 2 の Rho または c パラメータ |
| A, B, C, D | 2 つのジェネレーターからのマッピング可能な出力(別表参照) |
制御機能
| コントロール | 機能 |
|---|---|
| 左エンコーダー(回す) | 現在選択されているジェネレーターの周波数を増減する |
| 左エンコーダー(押す) | ジェネレーターの選択を切り替える |
| 右エンコーダー(回す) | ナビゲーションモード:メニュー項目を上下に移動する 値編集モード:編集中の値を増減する |
| 右エンコーダー(押す) | ナビゲーションモードと値編集モードの切り替え |
| 右エンコーダー(長押し) | アプリ選択メニュー |
| 「▲」ボタン(長押し) | スクリーンセーバーの起動 |
| 「▲」ボタン(押す) | 現在選択されているジェネレーターの周波数を 32 増加させる |
| 「▼」ボタン(押す) | 現在選択されているジェネレーターの周波数を 32 減少させる |
設定
| 設定 | 意味 |
|---|---|
| Freq 1 | ジェネレーター 1 の周波数/速度 範囲は0~255 |
| Freq 2 | ジェネレーター 2 の周波数/速度 範囲は 0〜255 |
| Rho/c 1 | ジェネレーター 1 の Rho (Lorenz アトラクター) または c (Rössler アトラクター) パラメータ |
| Rho/c 2 | ジェネレーター 2 の Rho (Lorenz アトラクター) または c (Rössler アトラクター) パラメータ |
| LFreq 1 Rng | Lorenz および Rössler ジェネレーター 1 の周波数/速度範囲 範囲は ‘sloth’, ‘lazy’, ‘slow’, ‘med’, ‘fast’ |
| LFreq 2 Rng | Lorenz および Rössler ジェネレーター 2 の周波数/速度範囲 範囲は ‘sloth’, ‘lazy’, ‘slow’, ‘med’, ‘fast’ |
| out A | 出力 A の出力マッピング(利用可能な選択肢は別表) |
| out B | 出力 B の出力マッピング(利用可能な選択肢は別表) |
| out C | 出力 C の出力マッピング(利用可能な選択肢は別表) |
| out D | 出力 D の出力マッピング(利用可能な選択肢は別表) |
Lorenz アトラクターと Rössler アトラクターのパラメータ Rho と c は、それぞれカオス発生系の変動の度合いを決定する。
この値は、関数が崩壊しないように制約されているが、極端な設定の組み合わせによっては、ジェネレーター機能が完全に崩壊することがある。
その場合は、Rho/c の設定を変更し、関連するトリガー入力に位相リセットのためのパルスを送信して、ジェネレーターをリセットする。
| 出力マッピング値 | 意味 |
|---|---|
| Lx1 | ジェネレーター 1 Lorenz アトラクター x 値 |
| Ly1 | ジェネレーター 1 Lorenz アトラクター y 値 |
| Lz1 | ジェネレーター 1 Lorenz アトラクター z 値 |
| Lx2 | ジェネレーター 2 Lorenz アトラクター x 値 |
| Ly2 | ジェネレーター 2 Lorenz アトラクター y 値 |
| Lz2 | ジェネレーター 2 Lorenz アトラクター z 値 |
| Rx1 | ジェネレーター 1 Rössler アトラクター x 値 |
| Ry1 | ジェネレーター 1 Rössler アトラクター y 値 |
| Rz1 | ジェネレーター 1 Rössler アトラクター z 値 |
| Rx2 | ジェネレーター 2 Rössler アトラクター x 値 |
| Ry2 | ジェネレーター 2 Rössler アトラクター y 値 |
| Rz2 | ジェネレーター 2 Rössler アトラクター z 値 |
| Lx1+Rx1 | ジェネレーター 1 Lorenz アトラクター x 値と ジェネレーター 1 Rössler アトラクター x 値の和 |
| Lx1+Rz1 | ジェネレーター 1 Lorenz アトラクター x 値と ジェネレーター 1 Rössler アトラクター z 値の和 |
| Lx1+Ly2 | ジェネレーター 1 Lorenz アトラクター x 値と ジェネレーター 2 Lorenz アトラクター y 値の和 |
| Lx1+Lz2 | ジェネレーター 1 Lorenz アトラクター x 値と ジェネレーター 2 Lorenz アトラクター z 値の和 |
| Lx1+Rx2 | ジェネレーター 1 Lorenz アトラクター x 値と ジェネレーター 2 Rössler アトラクター x 値の和 |
| Lx1+Rz2 | ジェネレーター 1 Lorenz アトラクター x 値と ジェネレーター 2 Rössler アトラクター z 値の和 |
| Lx1xLy1 | ジェネレーター 1 Lorenz アトラクター x 値と ジェネレーター 1 Lorenz アトラクター y 値のビットごとの XOR*4 |
| Lx1xLx2 | ジェネレーター 1 Lorenz アトラクター x 値と ジェネレーター 2 Lorenz アトラクター x 値のビットごとの XOR*4 |
| Lx1xRx1 | ジェネレーター 1 Lorenz アトラクター x 値と ジェネレーター 1 Rössler アトラクター x 値のビットごとの XOR*4 |
| Lx1xRx2 | ジェネレーター 1 Lorenz アトラクター x 値と ジェネレーター 2 Rössler アトラクター x 値のビットごとの XOR*4 |
スクリーンセーバー
スクリーンセーバーは、A および B 出力を画面の左半分に、C および D 出力を画面の右半分に、ベクトルスコープ(X/Y)で表示する。
Tips
X/Y(ベクトルスコープ)信号を表示できるオシロスコープを持っている場合は、どちらかのタイプのジェネレーターの X, Y, Z 出力のペアをオシロスコープにつなぎ、古典的で奇妙なアトラクターのパターンを観察してみるとよい。
Lorenz アトラクター と Rössler アトラクター
要するに「カオティック」なのね、ってことくらいしか分かってないけど。
Lorenz アトラクター
ローレンツ方程式(ローレンツほうていしき)とは、数学者・気象学者であるエドワード・ローレンツ(Edward Lorenz)が最初に研究した非線型常微分方程式である。特定のパラメータ値と初期条件に対してカオス的な解を持つことで注目されている。特に、ローレンツ方程式のカオス解の集合はローレンツ・アトラクターと呼ばれる。いわゆるバタフライ効果の説明に用いられることが多く、決定論的な連立常微分方程式が初期値鋭敏性を持つことは驚きをもって迎えられ、カオス研究の端緒となった。(中略)
Wikipedia「ローレンツ方程式」より引用
スメイルの14番目の問題は「ローレンツアトラクターはストレンジアトラクターの性質を持つか?」というものであった。この問題は2002年にウォリック・タッカーによって肯定的に解決された。(後略)
Rössler アトラクター
レスラー方程式(レスラーほうていしき、Rössler equation)とは、3次元の連続時間力学系の一種。(中略)
Wikipedia「レスラー方程式」より引用
西ドイツの化学者オットー・レスラーにより、1976年の論文 “An equation for continuous chaos” で最初に提唱された。レスラーは、1963年にアメリカの気象学者エドワード・ローレンツが発表したローレンツ方程式のカオスに触発され、ローレンツ方程式をより単純化した方程式からカオスが生み出されることを考察するために導入した。ローレンツ方程式は気体の熱対流の計算モデルから方程式を導いたのに対して、レスラー方程式は実在の物理現象をベースにせずカオスの研究のために作為的に導入されたものである。
カオスが発生するには、力学系は必ず非線形性を持つ必要があり、なおかつ連続時間力学系の場合は3変数以上が必要になる。レスラー方程式の非線形項は第3式目の xz のみとなっており、カオスを発生させる連続時間力学系の中でも非常に単純な非線形しか持たない点が特筆される。
レスラー方程式は特定のパラメータの範囲でストレンジアトラクターを持つ。特に、パラメータ a = 0.2、b = 0.2、c = 5.7 はレスラーにより最初に導入されたときのパラメータ値で、このパラメータ値のときのストレンジアトラクターはレスラー・アトラクタ(Rössler attractor)として良く知られている。このアトラクタの形は、メビウスの帯のような、リボンを一回ひねって両端を合わせた形になっている。(後略)
論理回路
※こちらのサイトを参考にさせていただきました。
| 論理回路 | 入力 A | 入力 B | 出力 X | |
|---|---|---|---|---|
| AND | 論理積 $X = A \cdot B$ | 0 | 0 | 0 |
| 0 | 1 | 0 | ||
| 1 | 0 | 0 | ||
| 1 | 1 | 1 | ||
| OR | 論理和 $X = A + B$ | 0 | 0 | 0 |
| 0 | 1 | 1 | ||
| 1 | 0 | 1 | ||
| 1 | 1 | 1 | ||
| NOT | 論理否定 $X = \bar{A}$ | 0 | – | 1 |
| 1 | – | 0 | ||
| XOR | 排他的論理和 eXclusive OR $X = A \oplus B$ | 0 | 0 | 0 |
| 0 | 1 | 1 | ||
| 1 | 0 | 1 | ||
| 1 | 1 | 0 | ||
| NAND | 否定論理積 (AND の結果を否定) | 0 | 0 | 1 |
| 0 | 1 | 1 | ||
| 1 | 0 | 1 | ||
| 1 | 1 | 0 | ||
| NOR | 否定論理和 (OR の結果を否定) | 0 | 0 | 1 |
| 0 | 1 | 0 | ||
| 1 | 0 | 0 | ||
| 1 | 1 | 0 | ||
どんな論理回路でも NAND または NOR だけで構成できる(NAND 論理の完全性 / NOR 論理の完全性)んですって。世界で初めてそれに気づいた人って、気づいたとき、どんな気持ちだったんだろう。
それはともかく、上の *4 について言えば、「どちらかがゼロの時だけ、ゼロじゃない方の位相に応じた電圧が出力される」と理解しておけばいいのかな。
あああああ、オシロスコープ欲しい。出力を波形で並べて「なるほど!」って納得したい!
やっぱり、普段「わかってないよなあ、わたし」って申し訳ない気持ちになりながら使っているものについて、ちゃんと調べて理解すると、アイディアも湧いてくるし、もっといろいろな使い方に、ひいてはもっといろいろな音作りに挑戦してみようという気にもなれる。やってよかった。まだまだわからないことも多いし、もっともっと知りたいこともたくさんあるけれど。
さあ、次は Piqued。
いちおう、わたしの無駄口を省いたバージョンを PDF にして置いておきます。
コピペして、体裁をちょっといじっただけなので、味も素っ気もないですけど。
こんなのでよければ、一部なり全部なり、ご自由にお使いください。








